1. 일차 함수, 기울기와 y절편
- 함수
- 두 집합 사이의 관계를 설명하는 수학 개념
- 변수 x와 y가 있을 때, x가 변하면 이에 따라 y가 어떤 규칙으로 변하는지를 나타냄
- 일차 함수
- y가 x에 관한 일차식으로 표현된 경우를 의미
- x가 일차인 형태로 남으려면, a는 0이 아니어야 함
- a는 기울기, b는 절편


딥러닝이란 x가 주어지고 원하는 y값이 있을 때, 적절한 a와 b를 찾는 것!
2. 이차 함수와 최솟값
- 이차 함수
- y가 x에 관한 이차식으로 표현되는 경우


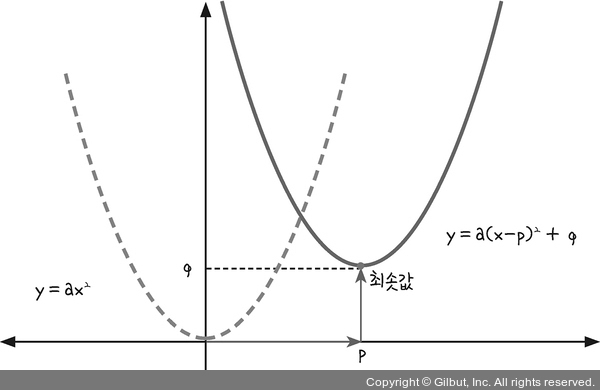
딥러닝에서는 최솟값을 찾아내는 과정이 매우 중요
최솟값은 '최소 제곱법' 공식을 사용해 구함
최소 제곱법을 계산하기 위해서는 미분과 기울기를 사용
3. 미분, 순간 변화율과 기울기

- a에서의 순간 변화율은 기울기
- 순간 변화율이란 a가 미세하게 움직였을때, y값 또한 미세하게 변화하는데 이런 순간적인 변화를 의미
- 미분을 하는 것은 순간 변화율을 구하는 것
- 미분 계수란 어느 순간에 어떤 변화가 일어나고 있는지 숫자로 나타낸 것




- 미분의 성질
- f(x) = x일 때 f '(x) = 1
- f(x) = a에서 a가 상수일 때 f '(x) = 0
- f(x) = ax에서 a가 상수일 때 f '(x) = a
- f(x) = xa에서 a가 자연수일 때 f '(x) = ax^(a-1)
- f(g(x))에서 f(x)와 g(x)가 미분 가능할 때 {f(g(x))}' = f '(g(x)) × g'(x)
4. 편미분
- 편미분
- 원하는 한 가지 변수만 미분하고, 그 외의 변수는 모두 상수로 취급
- f(x, y) = x^2 + yx + a일 때

5. 지수와 지수 함수
- 지수
- a를 밑이라 하고 그 위의 x을 지수
- 지수 함수에서는 밑이 중요


6. 시그모이드 함수
- 시그모이드 함수
- 지수함수에서 밑의 값이 자연 함수 e인 함수
- 0 또는 1, 두 개의 값 중 하나를 고를 때 유용하게 사용
- 참 거짓 판단에서 유용


7. 로그와 로그 함수
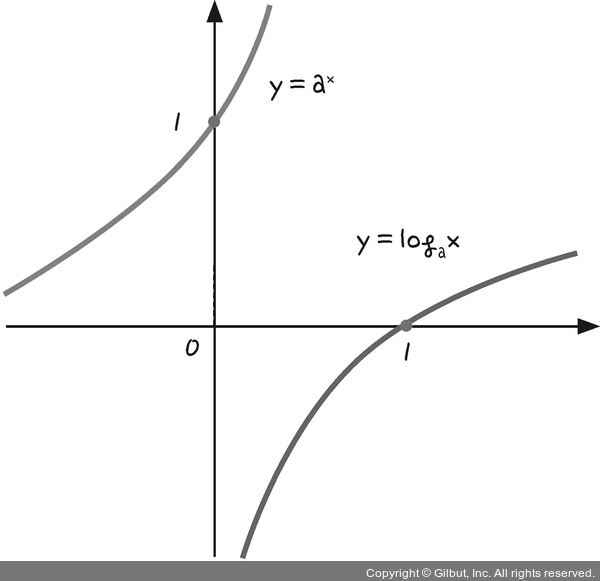
- 지수와 로그

- 지수 함수와 로그 함수는 역함수 관계
'ML > 모두의 딥러닝' 카테고리의 다른 글
| 5장) 참 거짓 판단 장치 : 로지스틱 회귀 (0) | 2023.07.10 |
|---|---|
| 4-2장) 다중 선형 회귀 (0) | 2023.07.07 |
| 4-1장) 오차 수정하기 : 경사 하강법 (0) | 2023.07.06 |
| 3장) 선형 회귀 (0) | 2023.07.06 |
| 1장) 나의 첫 딥러닝 (0) | 2023.07.05 |