1. 로지스틱 회귀(logistic regression)
- 참과 거짓 중 하나를 내놓는 과정
- 참과 거짓 사이를 구분하는 s자 형태의 선을 그려가는 작업
ex)
| 공부한 시간 | 2 | 4 | 6 | 8 | 10 | 12 | 14 |
| 합격 여부 | 불합격 | 불합격 | 불합격 | 합격 | 합격 | 합격 | 합격 |

2. 시그모이드 함수(sigmoid function)
- S자 형태로 그래프가 그려지는 함수로, 로지스틱 회귀를 풀 때 사용

- 구해야 하는 값은 ax+b
- a는 그래프의 경사도를 의미
- b는 그래프의 좌우 이동을 의미


따라서 a와 b에 따라 오차가 변함
a값이 작아지면 오차는 무한대로 커짐
그러나 a값이 커진다고 해서 오차가 무한대로 커지지 않음

b와 오차의 관계는 이차 함수 그래프와 유사한 형태로 나타남

3. 오차 공식
- 경사 하강법을 이용하여 a와 b를 구함
- 경사 하강법을 사용하기 위해선 먼저 오차를 구해야함
- 시그모이드 함수의 특징
- y값이 0과 1 사이
- 실제 값이 1일 때, 예측 값이 0에 가까워지면 오차가 커짐
- 반대인 경우도 마찬가지
→로그 함수를 사용하여 공식화

이를 수식으로 나타내면 다음과 같다.

실제 값을 y라 할 때, 이 값이 1이면 B부분이 사라짐
반대로 0인 경우에는 A부분이 사라짐
따라서 실제 값에 따라 두 함수를 각각 사용
Code)
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
#공부시간 X와 성적 Y의 리스트를 만듭니다.
data = [[2, 0], [4, 0], [6, 0], [8, 1], [10, 1], [12, 1], [14, 1]]
x_data = [i[0] for i in data]
y_data = [i[1] for i in data]
#그래프로 나타내 봅니다.
plt.scatter(x_data, y_data)
plt.xlim(0, 15)
plt.ylim(-.1, 1.1)
# 기울기 a와 절편 b의 값을 초기화 합니다.
a = 0
b = 0
#학습률을 정합니다.
lr = 0.05
#시그모이드 함수를 정의합니다.
def sigmoid(x):
return 1 / (1 + np.e ** (-x))
#경사 하강법을 실행합니다.
for i in range(2001):
for x_data, y_data in data:
a_diff = x_data*(sigmoid(a*x_data + b) - y_data)
b_diff = sigmoid(a*x_data + b) - y_data
a = a - lr * a_diff
b = b - lr * b_diff
if i % 1000 == 0: # 1000번 반복될 때마다 각 x_data값에 대한 현재의 a값, b값을 출력합니다.
print("epoch=%.f, 기울기=%.04f, 절편=%.04f" % (i, a, b))
# 앞서 구한 기울기와 절편을 이용해 그래프를 그려 봅니다.
x_data = [i[0] for i in data]
y_data = [i[1] for i in data]
plt.scatter(x_data, y_data)
plt.xlim(0, 15)
plt.ylim(-.1, 1.1)
x_range = (np.arange(0, 15, 0.1)) #그래프로 나타낼 x값의 범위를 정합니다.
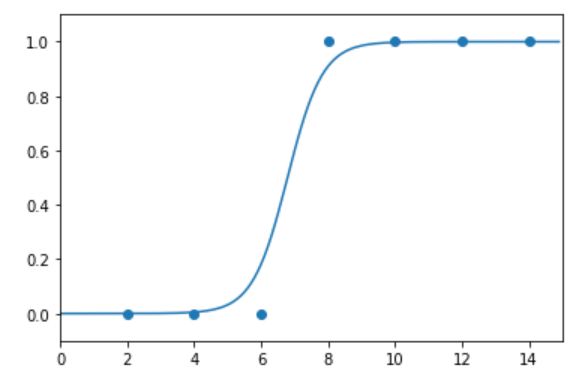
plt.plot(np.arange(0, 15, 0.1), np.array([sigmoid(a*x + b) for x in x_range]))
plt.show()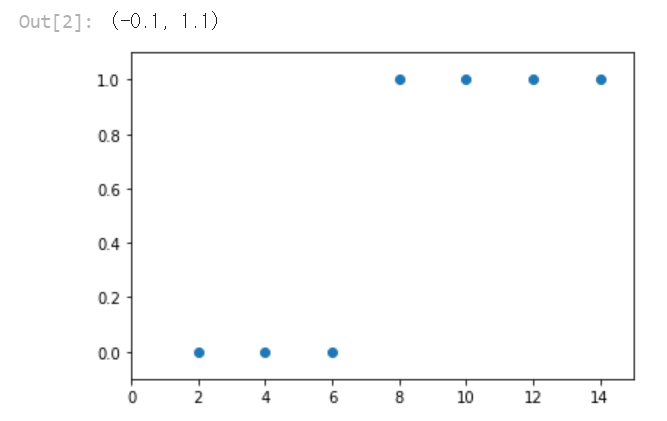

'ML > 모두의 딥러닝' 카테고리의 다른 글
| 7장) 다층 퍼셉트론 (0) | 2023.07.10 |
|---|---|
| 6장) 퍼셉트론 (0) | 2023.07.10 |
| 4-2장) 다중 선형 회귀 (0) | 2023.07.07 |
| 4-1장) 오차 수정하기 : 경사 하강법 (0) | 2023.07.06 |
| 3장) 선형 회귀 (0) | 2023.07.06 |