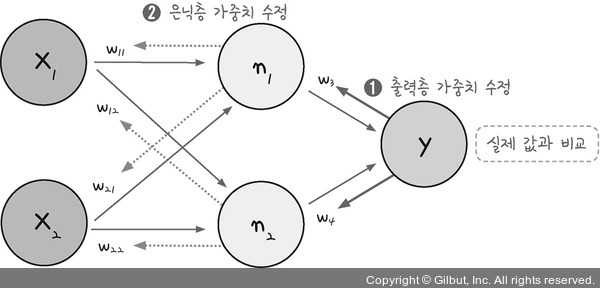
1. 오차 역전파(back propagation)
- 다층 퍼셉트론에서의 최적화 과정
- 결과값의 오차를 구해 하나 앞선 가중치를 차례로 거슬러 올라가며 조정
→ 최적화의 계산 방향이 출력층에서 시작하여 앞으로 진행 - 가중치에서 기울기를 빼도 값의 변화가 없을 때까지 계속해서 가중치 수정 작업을 반복
- 동작
- 임의의 초기 가중치 W를 준 뒤 결과를 계산
- 계산 결과와 우리가 원하는 값 사이의 오차를 계산
- 경사 하강법을 이용해 바로 앞 가중치를 오차가 작아지는 방향으로 업데이트
- 미분 값이 0에 가까워지는 방향으로 나아간다는 의미
- 위 고정을 더이상 오차가 줄어들지 않을 때까지 반복



2. XOR 문제를 오차 역전파 방식으로 해결하기
- 환경 변수 지정
- 환경 변수에는 입력 값과 타깃 결과값이 포함된 데이터셋, 학습률 등이 포함
- 활성화 함수와 가중치 등을 선언
- 신경망 실행
- 초기값을 입력하여 활성화 함수와 가중치를 거쳐 결과값이 나오게 함
- 결과를 실제값과 비교
- 오차를 측정
- 역전파 실행
- 출력층과 은닉층의 가중치를 수정
- 결과 출력
Code)
import random
import numpy as np
random.seed(777)
# 환경 변수 지정
# 입력값 및 타겟값
data = [
[[0, 0], [0]],
[[0, 1], [1]],
[[1, 0], [1]],
[[1, 1], [0]]
]
# 실행 횟수(iterations), 학습률(lr), 모멘텀 계수(mo) 설정
iterations=5000
lr=0.1
mo=0.4
# 활성화 함수 - 1. 시그모이드
# 미분할 때와 아닐 때의 각각의 값
def sigmoid(x, derivative=False):
if (derivative == True):
return x * (1 - x)
return 1 / (1 + np.exp(-x))
# 활성화 함수 - 2. tanh
# tanh 함수의 미분은 1 - (활성화 함수 출력의 제곱)
def tanh(x, derivative=False):
if (derivative == True):
return 1 - x ** 2
return np.tanh(x)
# 가중치 배열 만드는 함수
def makeMatrix(i, j, fill=0.0):
mat = []
for i in range(i):
mat.append([fill] * j)
return mat
# 신경망의 실행
class NeuralNetwork:
# 초깃값의 지정
def __init__(self, num_x, num_yh, num_yo, bias=1):
# 입력값(num_x), 은닉층 초깃값(num_yh), 출력층 초깃값(num_yo), 바이어스
self.num_x = num_x + bias # 바이어스는 1로 지정(본문 참조)
self.num_yh = num_yh
self.num_yo = num_yo
# 활성화 함수 초깃값
self.activation_input = [1.0] * self.num_x
self.activation_hidden = [1.0] * self.num_yh
self.activation_out = [1.0] * self.num_yo
# 가중치 입력 초깃값
self.weight_in = makeMatrix(self.num_x, self.num_yh)
for i in range(self.num_x):
for j in range(self.num_yh):
self.weight_in[i][j] = random.random()
# 가중치 출력 초깃값
self.weight_out = makeMatrix(self.num_yh, self.num_yo)
for j in range(self.num_yh):
for k in range(self.num_yo):
self.weight_out[j][k] = random.random()
# 모멘텀 SGD를 위한 이전 가중치 초깃값
self.gradient_in = makeMatrix(self.num_x, self.num_yh)
self.gradient_out = makeMatrix(self.num_yh, self.num_yo)
# 업데이트 함수
def update(self, inputs):
# 입력 레이어의 활성화 함수
for i in range(self.num_x - 1):
self.activation_input[i] = inputs[i]
# 은닉층의 활성화 함수
for j in range(self.num_yh):
sum = 0.0
for i in range(self.num_x):
sum = sum + self.activation_input[i] * self.weight_in[i][j]
# 시그모이드와 tanh 중에서 활성화 함수 선택
self.activation_hidden[j] = tanh(sum, False)
# 출력층의 활성화 함수
for k in range(self.num_yo):
sum = 0.0
for j in range(self.num_yh):
sum = sum + self.activation_hidden[j] * self.weight_out[j][k]
# 시그모이드와 tanh 중에서 활성화 함수 선택
self.activation_out[k] = tanh(sum, False)
return self.activation_out[:]
# 역전파의 실행
def backPropagate(self, targets):
# 델타 출력 계산
output_deltas = [0.0] * self.num_yo
for k in range(self.num_yo):
error = targets[k] - self.activation_out[k]
# 시그모이드와 tanh 중에서 활성화 함수 선택, 미분 적용
output_deltas[k] = tanh(self.activation_out[k], True) * error
# 은닉 노드의 오차 함수
hidden_deltas = [0.0] * self.num_yh
for j in range(self.num_yh):
error = 0.0
for k in range(self.num_yo):
error = error + output_deltas[k] * self.weight_out[j][k]
# 시그모이드와 tanh 중에서 활성화 함수 선택, 미분 적용
hidden_deltas[j] = tanh(self.activation_hidden[j], True) * error
# 출력 가중치 업데이트
for j in range(self.num_yh):
for k in range(self.num_yo):
gradient = output_deltas[k] * self.activation_hidden[j]
v = mo * self.gradient_out[j][k] - lr * gradient
self.weight_out[j][k] += v
self.gradient_out[j][k] = gradient
# 입력 가중치 업데이트
for i in range(self.num_x):
for j in range(self.num_yh):
gradient = hidden_deltas[j] * self.activation_input[i]
v = mo*self.gradient_in[i][j] - lr * gradient
self.weight_in[i][j] += v
self.gradient_in[i][j] = gradient
# 오차의 계산(최소 제곱법)
error = 0.0
for k in range(len(targets)):
error = error + 0.5 * (targets[k] - self.activation_out[k]) ** 2
return error
# 학습 실행
def train(self, patterns):
for i in range(iterations):
error = 0.0
for p in patterns:
inputs = p[0]
targets = p[1]
self.update(inputs)
error = error + self.backPropagate(targets)
if i % 500 == 0:
print('error: %-.5f' % error)
# 결괏값 출력
def result(self, patterns):
for p in patterns:
print('Input: %s, Predict: %s' % (p[0], self.update(p[0])))
if __name__ == '__main__':
# 두 개의 입력 값, 두 개의 레이어, 하나의 출력 값을 갖도록 설정
n = NeuralNetwork(2, 2, 1)
# 학습 실행
n.train(data)
# 결괏값 출력
n.result(data)
# Reference: http://arctrix.com/nas/python/bpnn.py (Neil Schemenauer)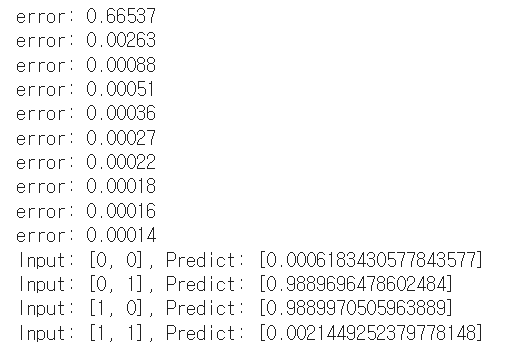
'ML > 모두의 딥러닝' 카테고리의 다른 글
| 10장) 모델 설계하기 (0) | 2023.07.10 |
|---|---|
| 9장) 신경망에서 딥러닝으로 (0) | 2023.07.10 |
| 7장) 다층 퍼셉트론 (0) | 2023.07.10 |
| 6장) 퍼셉트론 (0) | 2023.07.10 |
| 5장) 참 거짓 판단 장치 : 로지스틱 회귀 (0) | 2023.07.10 |